Topological Barcodes and Subsets of Normals

Topological data analysis generates barcodes as a means to determine the length of persistent homologies found in sample data. I’ve drawn tori and cyclides over normal distributions in several earlier posts. The tori happen when the distribution is normal. The cyclides happen when the distribution is pre-normal. Sample size drives the distribution from hyperbolic space to Euclidean space, and from Euclidean space to spherical space. The distribution is differential. I have yet to find that to be the case in topological data analysis. I don’t find that statistical distributions are differential either. But, I have found that in a recent study of Covid patients where machine learning was applied to determine treatment outcomes of individual patients, the geometries of the spaces were in conflict. The samples were prenormal, or happening in hyperboic space while machine learning happens in Euclidean space. Doing machine learning in hyperbolic spaces is a contemporary research topic. We assert normality long before normality is actually achieved. We don’t pay attention to how sample size drives the properties of the sample spaces. That tradition of considering distributions to be static and non-differential continues in topological data analysis.

I’ve been looking at convergence to tail situations. Much of the discussion is about knowing the mean and the standard deviation, both of which are unknowable in the distributions having the convergence to tail problem. So in this morning’s research, I found that outliers alter the topological barcodes or persistent homology of the distribution.

I’ve mentioned how a subset of a normal distribution might have a sample size too small to remain normal. These subsets happen in hyperbolic space.

I did find Persistent homology of Gaussian fields in Euclidean space this morning. That article mentioned this article, Understanding Persistent Homology and PLEX Using a Networking Dataset. The latter study used subsets as the basis for a collection of tori each having their own persistent homology, a length. Outliers impact the length of the persistent homology. The outliers impact the regression to tail situations. Perhaps we should look at the homology rather than a mean and a standard deviation that we cannot compute.

The study sought out subsets of brain function data to find evidence of various brain pathologies.The brain is seen as a manifold, so an atlas is used to map brain function data to collections of dimensions. Those dimensions have their own normal. Each of those normals appear in the diagram as a tail. Each of those tails drive the shape of the torus related to each of those tails. Each of those normals represent a subset of the sample data. Those subsets are defined by the atlases describing the brain’s manifold.

The thinking of a corporation could be represented by a cognitive manifold.

One interesting aspect of the subset as torus view is that the length of the persistent homology tells us the radius of the tori. In earlier discussions, I found that a skewed distribution has a short tail and long tail pair. That pair of tails is expressed by a cyclide where the smaller diameter of the short tail increases to the larger diameter of the long tail as the diameter rotates around the normal. This is what makes the pre-normal generate a cyclide, rather than a torus. Rotating away from the long tail shrinks the diameter. This orients the dimension without the need for a correlation.

Looking at the persistent homology’s length provides us with a better way to see the impact of outliers. The orientation of the cyclide provides us with a way to se the orientation of the underlying dimension in a pre-normal space.

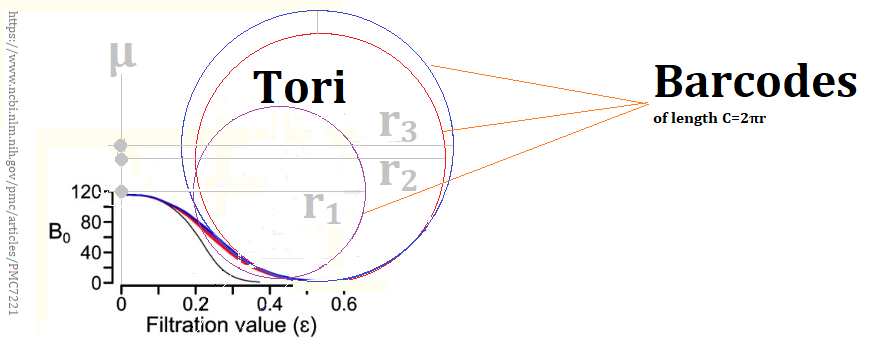
Here I am just showing a slice through the three doughnuts or tori generated by the three subset samples. The curvature and eccentricity of the distributions generate the fitness of the tori and the normal.

Enjoy.