Poincaré Disk

The Poincaré is one model of hyperbolic space. Try it out here.

Infinity is at the edge of the Poincaré disk, aka the circle. The Poincaré is a three more dimensional bowl seen from above. Getting where you want to go requires traveling along a hyperbolic geodesic. And, projecting a future will understate your financial outcomes. Discontinuous innovation happens here.

A long time ago, I installed a copy of Hyperbolic Pool. I played it once or twice. Download it here. My copy is installed. It say go there. Alas, it did not work when I tested it from this post. My apologies. Hyperbolic space was a frustrating place to shoot some pool.

I’ve done some research. More to do.

A few things surprised me today. The Wikipedia entry for Gaussian Curvature has a diagram of a torus. The inner surfaces of the holes exhibit negative curvature. The outer surfaces of the torus exhibits positive curvature. That was new to me.

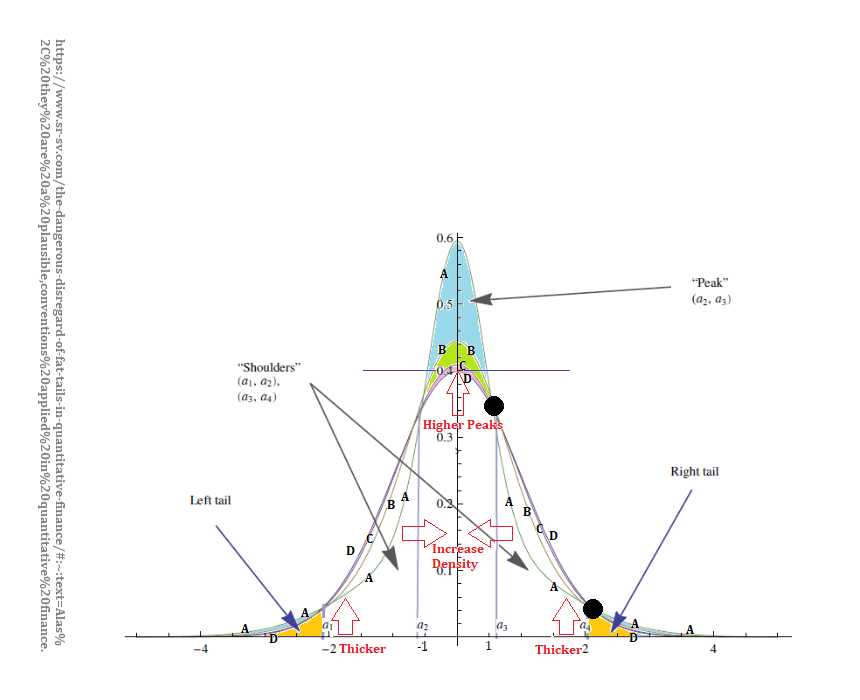
I’ve blogged on tori and cyclides in the context of long and short tails of pre-normal, normal distributions, aka skewed kurtotic normal distributions that exit before normality is achieved. These happen while the mean, median, and mode have not converged. I’ve claimed that the space where this happens is hyperbolic from the random variable’s birth after the Dirac function that happens when random variable is asserted into existence and continues until the distribution becomes normal.

Here are the site search results for

• curvature
• torus
• cyclide

There will be some redundancy across those search results. In these search results, you will find that I used the term spherical space. I now us the term elliptical space instead.

We don’t ever see hyperbolic space. We insist that we can achieve normality in a few data points. It takes more than 2¹¹ data points to achieve normality. We believe the data is in Euclidean “ambient” space. We do linear algebra in that ambient space, not in hyperbolic space. Alas, the data is not in ambient space. The space changes. Euclidean space is fleeting: waiting at n-1, arrival at n, departing at n+1, but computationally convenient. Maybe you’ll take a vacation, so the data collection stalls, and until you get back, your distribution will be stuck in hyperbolic space waiting, waiting, waiting to achieve actual normality.

Statistics insists on the standard normal. We assert it. Then, we use the assertion to prove the assertion.

Machine learning, being built on neurons and neural nets, insists on the ambient space because Euclidean space is all their neurons and neural nets know. Euclidean space is convenient. Curvature in machine learning is all kinds of inconvenient. Getting funded is not just a convenience. It might be the wrong thing to do, but we do much wrong these days. Restate your financials, so the numbers for the future, from elliptical space paint a richer future than the hyperbolic numbers that your accounting system just gave you.

And one more picture. This from a n-dimensional normal, a collection of Hopf Fibered Linked Tori. Fibered, I get, but I stayed out of it so far. Linked happens, but I’ve yet to read all about it.

The thin torus in the center of the figure results from a standard normal in Euclidean space. Its distribution is symmetrical. Both of its tails are on the same dimensional axis of the distribution. They have the same curvature. The rest of the dimensions have a short tail and a long tail. Curvature is the reciprocal of the radius. The fatter portion of the cyclides represent the long tails. Long tails have the lowest curvatures. The thinner portion of the cyclides represent the short tails. Short tails have the highest curvatures. Every dimension has two tails in the we can only visualize in 2-D sense. These tori and cyclides are defined by their tails.

Keep in mind that the holes of the tori and cyclides are the cores of the normals. The cores are not dense with data. Statistical inference is about tails. And, regression to tails are about tails, but in the post-Euclidean, elliptical space, n+m+1 data point sense. One characteristic of the regression to tails, aka thick-tailed distributions, is that their cores are much more dense than that of the standard normal.

Hyperbolic space will only show up on your plate if you are building a market for a discontinuous innovation. Almost none of you do discontinuous innovation, but even continuous innovation involves elliptical space, rather than the ambient Euclidean space, or the space of machine learning. We pretend is that Euclidean space is our actionable reality. Even with continuous innovation, the geometry of that space matters.

Enjoy!

 
 
 
 
 
 
 
 
 
 
…

Thick Tails, et.al.

I’ve been focusing on regression to tails for while now. I came across an article, The dangerous disregard for fat tails in quantitative finance. Finding the mean and the standard deviation is hard. Thick tail distributions are unlike normal distributions. Normal distributions are usually assumed and underly linear regression.

I’ve taken a data view, rather than a dataset view. From that perspective, I could see that skewed normals happen when the dataset is too small to have achieved normality. When we assert the existence of a random variable, a Dirac function produces a vertical line to infinity. Then, we sample a sequence of values for that random variable. As a line, there is no probability, but as we sample the line becomes an interval, so we begin to have a distribution and probabilities. That distribution has a peak at some height. As the sample size increases, the height of distribution decreases. Once the data actually achieves normality, the height of the distribution falls, typically, to a value of 0.4.

The next figure stood out. The height of the distribution is 0.6. The distribution has already achieved normality. It is not a distribution on its way to achieving normality. The figure is based on a standard normal. Then, three thick-tailed distributions are overlaid on that standard normal. The thick-tail distributions have heights higher than a standard normal.

A straight line sits at the peak of the standard normal. The shape of the standard normal is labeled D. The three thick-tail distributions are labeled A, B, and C. The peak for distribution A is light blue; B is green; C is pink. The upper black dot is where thick-tailed distributions are thinner than the standard normal. Where they are thinner, they are inside the standard normal compressing the probability mass. The lower black dot is where the tails of the thick-tailed distributions are fatter than the standard normal and get back outside the standard normal.

The red arrows show how the probability mass moves. The probability mass inside one standard deviation from the mean increases from 68 percent to something between 75 to 90 percent.

The sampling process begins with the first sample. The distribution is in hyperbolic space. The process continues. Eventually, the sample achieves normality. The mean, median, and mode converge when normality is achieved. The distribution is in Euclidean space. As the sampling process continues, the standard deviation increases and the distribution is in spherical space. We, however, assume Euclidean space throughout.

I drew the next figure to illustrate the first paragraph on the page following the figure in the article that I used as the basis or the first figure in this post.

Each circle is one standard deviation larger than the circle inside it. The gold denotes the area three standard deviations from the mean or the extent of the standard normal. The space here is Euclidean. The Markov chain connects to linked events, black dots, that cascade into catastrophe.

At six standard deviations, the light blue circle is representative of an area out in the thick tail. This area would be elliptic, rather than circular. A lone single event, black dot, can cause a catastrophe. The space here is spherical.

The labels a1, a2, a3, and a4 refer back to the first figure where they inform us about the shoulders and tails of the thick-tailed distribution.

Log-normal distribution

The log-normal distribution is a thick-tailed distribution. IT is used as a first example. If your data is logarithmic, then this is the distribution to use. I’ve written about this distribution in the past. And I’ve posted this figure before. This time, the curve that the normal is reflected through is important.

A little Non-Euclidean Geometry

Teenagers get taught this stuff in high school these days. Expect to see more of it. While I was looking for regression to tail content, I came across Inversion in Circle on the Non-Euclidean Geometry blog. It mentions reflecting a triangle in a [straight] line with the next figure..

The orientation arrows change direction, otherwise, it is Euclidean on both sides of the straight line. That the line is straight is important. Curves change the results.

The orientation changes just like it did in the straight line case. The curve gives a particular result. The original triangle was Euclidean. The reflected triangle is hyperbolic. Well, that might take some calculations to prove that claim. The typical hyperbolic triangle is concave on all three sides. But, here A’B’ is convex. A spherical triangle is convex on all three sides. Draw straight lines for triangle A’B’C’. That is a Euclidean triangle. The straight line A’B’ is an interface between the hyperbolic and spherical spaces.

The normal distribution serves a purpose, and its triangle is thin or momentary. Before that distribution achieves normality the triangle was hyperbolic. One data point later, the distribution achieves normality and enters Euclidean space. Then, with the next data point, the distribution becomes spherical.

Next, I annotated the above figure.

I labelled the three spaces involved with the inversion. Pink represents the hyperbolic space. Grey represents the hyperbolic space. Blue represents spherical space.

The angles of a hyperbolic triangle sum to less than 180 degrees. The angles of a spherical triangle sum to more than 180 degrees. The purple numbers represent areas. The triangle would be spherical if A1+A2-A3>0, or hyperbolic if A1+A2-A3<0.

Space matters. When VCs do their analysis of discontinuous innovations, they do that analysis in Euclidean space. But, they are doing that analysis before normality is achieved, so their analysis understates the future proceeds. Given the understated numbers, they do not invest. That is a product management issue.

Other distributions

The first article that I cited in this post went on to compare a high variance Gaussian distribution and a Pareto distribution. The Gaussian distribution is stable.

The Pareto distribution converges to three different y values. I added triangles to represent the underlying logic of the associated each y-axis. It’s more important to see that the point of convergence is later in time each time the y-axis is changed.

Enjoy!

 
 
 
 
 
 
 
 
 
 
…